ЖЕСТКОПЛАСТИЧЕСКИЕ АРМИРОВАННЫЕ
ТОРОИДАЛЬНЫЕ ОБОЛОЧКИ
А.В. Налимов
В настоящее время все более широкое применение находят конструкции из композиционных материалов волокнистого строения, например, стеклопластиков, органопластиков, углепластиков, гибридных композиционных материалов и т.д. Для обеспечения эффективности таких конструкций необходимо выбирать структуры армирования и геометрические параметры так, чтобы выполнялись некоторые критерии определяемые условиями эксплуатации. Одним из таких критериев является значение предельно допустимых нагрузок для рассматриваемой конструкции.
Данная работа посвящена решению задачи о предельно допустимых нагрузках (расчет прочности) для тороидальных оболочек при заданных структурах армирования и геометрических параметров.
Одной из основных задач механики деформируемого твердого тела является задача определения предельно допустимой нагрузки для конструкций. Решению таких задач посвящено множество работ, где для описания поведения среды в предельном состоянии используются различные модели [1]. Одной из широко используемых моделей, описывающих поведение материала в предельном состоянии, является модель жесткопластических сред [2]. Эта модель описывает поведение материала конструкций при реализации в нем предельного состояния, а для определения предельных нагрузок сформулированы кинематическая и статическая теоремы [3]. В общем случае для определения несущей способности при помощи кинематической и статической теорем необходимо знать механизм пластического течения и область материала конструкции
, в которой реализуется пластическое течение [1]. Задача определения этих областей, в общем случае, не сформулирована [1].В работе на примере армированных тороидальных оболочек сформулированы системы уравнений для определения несущей способности как при реализации пластического течения во всем пролете оболочки, так и при и реализации его только в некоторой части оболочки. Проведен анализ влияния геометрических размеров и структур армирования на несущую способность, а также на изменения механизма пластического течения.
Исследованию предельного состояния оболочек вращения, выполненных из жесткопластического материала, посвящен ряд работ [4,6]. Тороидальные оболочки рассматривались только в работе [6], где приближенные решения для оболочек, выполненных из изотропного материала, были получены кинематическим методом. При этом предполагалось, что при x = ± p / 2
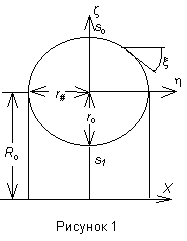
(рисунок 1) имеет место шарнирное опирание, т.е. рассматривался только сектор тора с шарнирно опертыми краями, и во всем пролете реализуется пластическое течение.
Поверхность текучести для армированных оболочек регулярно-однородного строения в случае, когда материал связующего подчиняется кусочно-линейному условию пластичности, образована пересечением ряда гиперплоскостей, предельные соотношения для которых в пространстве обобщенных напряжений определяются соотношениями [7]:
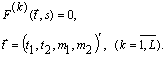 (1)
(1)
Ассоциированный закон течения при реализации одной из гиперплоскостей (1) записывается следующим образом [7]:
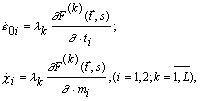 (2)
(2)
где
![]()
Если напряженное состояние соответствует ребру предельной поверхности, образованному пересечением двух или более гиперплоскостей (1), вектор скорости деформаций
С целью исключения из разрешающих уравнений неизвестного множителя l
k введем величину q [7]: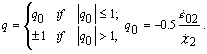 (3)
(3)
Согласно (2),(3) предельные соотношения (1) можно записать в виде [7]:
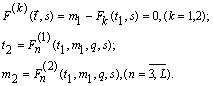 (4)
(4)
В дальнейшем ограничимся оболочками постоянной толщины
2H(s)=const, срединная поверхность которых образована вращением эллипса вокруг оси Х (рис.1). Армирующие волокна уложены вдоль траекторий, составляющих угол ± Y (s) с меридианом {± Y (so+ds)=± Y (so-ds), [ds=0¸ (s1-so)]}. Рассматриваемые тороидальные оболочки нагружены внутренним давлением Р(s)=const и массовой силой, вызванной вращением вокруг оси Х с угловой скоростью w о.В силу симметрии строения и нагружения относительно плоскости
Х=0 далее будем рассматривать только часть оболочки при sÎ [ so, s1] . Уравнения равновесия для осесимметричных тороидальных оболочек можно привести к виду [8]: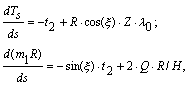 (5)
(5)
где
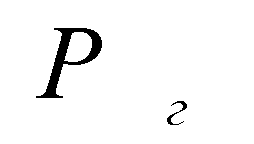
R, R
о - расстояние от оси Х до срединной поверхности оболочки и центра эллипса, образующего тороидальную оболочку, соответственно; x - угол между осью Х и касательной к меридиану; s о- константа, имеющая размерность напряжения; r *-плотность материала оболочки, отнесенная к плотности связующего r с; l о- предельный параметр нагружения (коэффициент запаса прочности); w о - скорость вращения оболочки; P - значение действующего внутреннего давления.Рассмотрим теперь случаи реализации в оболочке различных режимов, характеризующихся выполнением различных гиперплоскостей.
Реализация гиперплоскостей (4) с номерами
k=1,2 в некоторой части оболочки согласно кинематическим соотношениям [8] и закону течения (2) соответствует перемещению этой части как жесткого целого. Выполнение соотношения (4) (k=1,2) в некотором сечении s=s+ пластической области сопровождается реализацией пластического шарнира [9].При реализации в части пролета оболочки гиперплоскости с номером
n=3,...,L, из кинематических соотношений [2,8] и соотношений (2),(3) получим: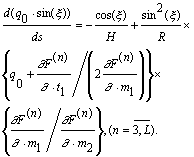 (6)
(6)
Уравнения (4)-(6) образуют систему трех нелинейных дифференциальных уравнений с неизвестным параметром l
о, описывающих распределение величин Ts,m1,q в области реализации пластического режима с номером n=3,...,L.В общем случае в пределах пролета оболочки может реализоваться некоторый набор пластических режимов, отвечающих различным гиперплоскостям, жесткие области и пластические шарниры. Поэтому для построения полной разрешающей системы уравнения (4)-(6) необходимо дополнить условиями сопряжения, а также сформулировать краевые условия.
Рассмотрим условия сопряжения различных пластических режимов. Отметим, что сопряжение различных пластических режимов может сопровождаться реализацией пластического шарнира и без него.
1. При сопряжении в сечении
s=s+ двух пластических режимов, отвечающих гиперплоскостям с номерами m и l (m¹ l;m,l=3,...,L), без пластического шарнира в соответствии с (4)-(6) получим следующие условия сопряжения:![]()
![]()
Здесь квадратные скобки обозначают скачок функции, а последнее соотношение получено из условии
![]() (
(
2. При реализации пластического шарнира в некотором сечении
s=s+ области, находящейся в состоянии течения, согласно (2), (5) имеют место следующие условия сопряжения:![]()
![]()
![]()
Прежде чем формулировать краевые условия отметим, что существуют, по крайней мере, две возможные схемы пластического течения оболочки. Одна схема характеризуется тем, что вся оболочка находится в пластическом состоянии, а во втором случае пластическое течение реализуется только в ее части.
В первом случае для формулировки задачи предельного равновесия необходимо задать четыре условия при
s=so, s=s1 в величинахВ силу симметрии оболочки, а также (3) и кинематическим соотношениям [8], краевые условия можно записать в виде:
![]()
Знак в значении для величины
q определяется в соответствии с характером деформирования оболочки.Кроме этого, возможны ситуации, когда при
s=so или (и) s=s1 реализуется пластический шарнир. В этих случаях согласно (8),(9) краевые условия записываются следующим образом:![]()
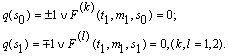
В случае, когда пластическое течение реализуется в части оболочки для определения несущей способности достаточно построить решение только в пластической области [10]. Отметим, что в общем случае можно построить несколько таких решений, например, пластическое состояние реализуется при
sÎ [so-s+,so+s+] и при sÎ [s1-sх,s1+sх] (рис.1). Значения предельных параметров нагружения полученные при решении этих задач будут различаться. Поскольку в соответствии с моделью жесткопластического тела история нагружения не влияет на значение предельной нагрузки [2,10], то истинным механизмом течения является тот, который реализуется при меньшей предельной нагрузке. Таким образом, для решения задачи при реализации пластического состояния в части оболочки необходимо задать шесть краевых условий в величинахЕсли пластическое состояние реализуется в части оболочки при
sÎ (s0,s+);so<s+<s1 или sÎ (s+,s1);so<s+<s1, то краевые условия согласно (2),(10) записываются в виде [9]:![]()
![]() ;
;
или
![]()
![]()
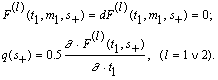
Если же пластическое состояние реализуется при
sÎ (sх,s+); so<s+,sx<s1, то на краях пластической области при s=s+ и s=sх выполняются последние три условия (11):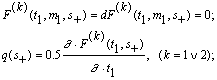
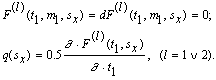
Система уравнений (4)-(6) с условиями сопряжения (7)-(8) и краевыми условиями типа (9) или (10) ((11)
,(12)) представляет собой многоточечную краевую задачу для системы нелинейных дифференциальных уравнений третьего порядка с параметром l о. Особенность этих задач заключается в том, что заранее не известны гиперплоскости, которые реализуются в пролете оболочки, их число, последовательность и области определения. Если решение этой многоточечной краевой задачи проводить методами [11-12], то выбор последовательности реализующихся режимов можно проводить путем перебора при условии, что вектор обобщенных напряжений не должен выходить за пределы поверхности текучести (1). Отметим, что при решении нелинейных краевых задач [11-12] необходимо задавать начальное приближение. Такое приближение нужно задавать для каждой комбинации режимов, что в связи с большим числом параметров сделать достаточно сложно. В принципе можно решить эту проблему, если в качестве начального приближения использовать решения упругой задачи или решения, полученные на основе некоторых упрощений. В принципе такая процедура реализуема, но она является достаточно сложной по логике и технике построения.Еще одной проблемой при решении этой задачи является то, что перед решением задачи необходимо определить механизм пластического течения, т.е. реализуется пластическое течение во всем пролете оболочки
Эта процедура реализована на языке Фортран, где при решении использовался дискретный метод продолжения по параметру [13], для решения нелинейной краевой задачи использовался метод колло-каций [12] и для выбора последовательности реализующихся режимов - метод последо-вательных приближений.
В качестве примера рассматривались оболочки со следующими геометрическими параметрами (рис.1):
H/Ro=0,001; ro=b × Ro; r#=a × Ro, где a -определяется при фиксированном значении параметра b из условия постоянства внутреннего объема (в качестве эталона использовалась оболочка при a =b =0,1). Оболочки изготовлены из многослойного армированного материала, в каждом из слоев которого армирующие элементы уложены вдоль траекторий, составляющих угол ± y ( s) = const с меридианом; интенсивности армирования определяются из условия постоянства сечения волокон и суммарного армирующего материала, где для эталона было полагалось w арм(s1)=0,6; s a± /s o=P/s o=100, где s a± ,s o- пределы текучести армирующих элементов при растяжении-сжатии и материала изотропного связующего, подчиняющегося условию пластичности Треска.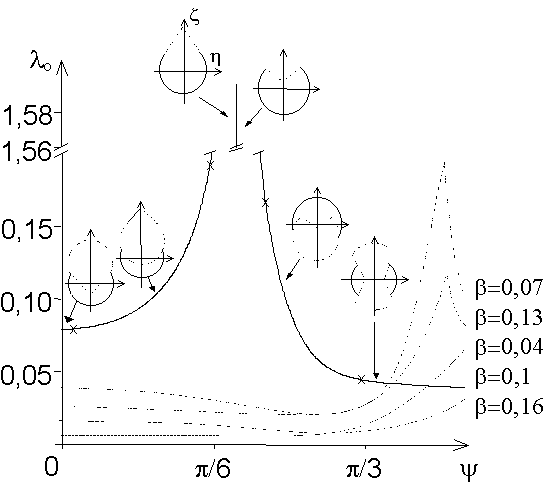
На рисунке 2 приведены зависимости параметра нагружения l о от угла укладки армирующих элементов y и при различных значениях геометрического параметра b для оболочек, нагруженных только внутренним давлением (w о =0). При b =0,1 схематично показаны механизмы течения оболочки, где сплошной линией приведено сечение тора, а штриховой - механизм движения. При y £ p / 6; y ³ 2 p / 9 пластическое состояние реализуется во всем пролете оболочки, а во всех остальных случаях решения получены при наличии жестких областей, где пластический шарнир реализуется в сечении
При других значениях параметра b
(b =0,07; b =0,13) (рисунок 2) максимальное значение параметра нагружения достигается при реализации в сечении s=sо также строго безмоментного напряженного состояния. При b =0,1, y » p / 6 0 во всей оболочке реализуется пластическое состояние и вектор обобщенных напряжений всюду соответствует ребрам поверхности текучести, образованным пересечением гиперповерхностей с номерами k=1Ú 2 и n=3,...,L (1), а вектор скоростей деформаций ортогонален поверхности с номером n. Следует отметить, что в работе [15] было сделано предположение, что в оболочках минимального веса реализуется напряженное состояние, соответствующее таким ребрам. В соответствии с полученными решениями (рисунок 2) это предположение [15] не соответствует действительности.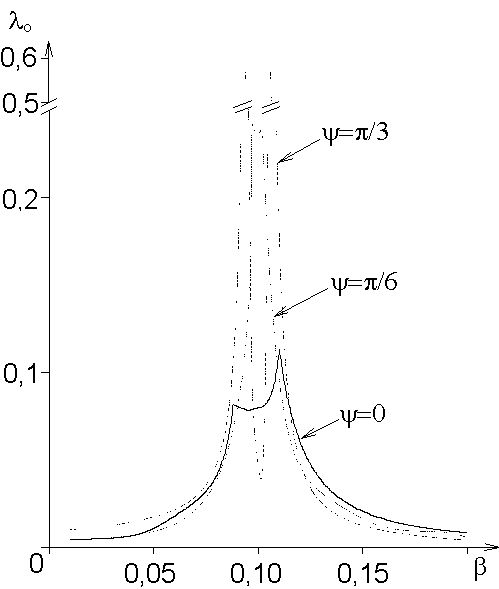
На рисунке 3 приведены зависимости параметра нагружения l
о от геометрического параметра b при различных структурах армирования (w о=0). В этом случае наибольшая несущая способность достигается при реализации строго безмоментного напряженного состояния в сечениях s=sо или s=s1, а также при реализации в конструкции нескольких пластических шарниров.Из рисунка 2-3 следует, что соответствующим подбором геометрических и структурных параметров несущую способность тороидальных оболочек можно существенно увеличить.
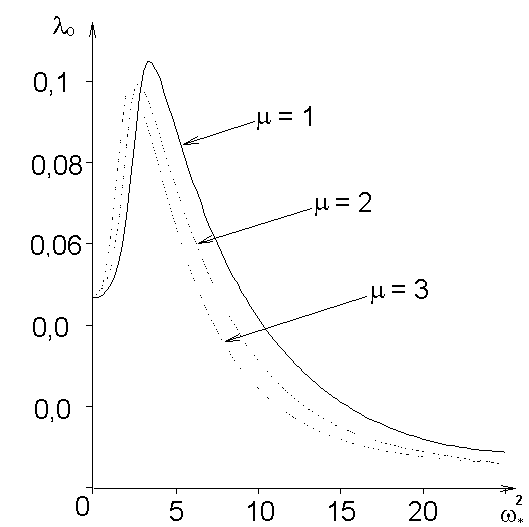
На рисунке 4 приведены зависимости параметра нагружения тора
(b =0 ,1; y = p /3) от скорости вращения (параметраСледует отметить, что ни в одном из рассмотренных случаев не получено решения, при котором
q(Ro)=m1(Ro)=0, что соответствует условиям, принятым в работе [3].На примере полученных точных решений задачи о несущей способности армированных тороидальных оболочек показано, что путем управления структурами армирования и геометрическими параметрами предельную нагрузку можно существенно увеличить. При воздействии на оболочку нескольких типов нагрузок, увеличение одной из них может привести как к повышению несущей способности так и к ее понижению. Путем подбора схемы армирования, геометрических параметров можно обеспечить различные механизмы течения конструкции.
Литература