ИНТЕРВАЛЬНАЯ КИНЕТИКА ХИМИЧЕСКИХ РЕАКЦИЙ.
ОДНОВРЕМЕННОЕ ОПРЕДЕЛЕНИЕ НЕСКОЛЬКИХ
КИНЕТИЧЕСКИХ ХАРАКТЕРИСТИК
ОБРАТИМОГО ПРОЦЕССА
В.М. Белов, В.В. Евстигнеев, В.А. Суханов, В.П. Смагин
В работе продолжено обсуждение моделей и методов интервальной кинетики химических реакций как раздела формальной кинетики. Перечислены группы интервальных моделей химической кинетики. Дано обоснование методики взвешенных эллипсоидов неопределенности в двумерном случае с использованием стандартных методов математической статистики. На примере обратимыхреакций первого порядка проведен одновременный расчет нескольких кинетических характеристик по выбранной методике.
На темы интервальной кинетики химических реакций уже был опубликован ряд работ, например [1-9]. Целью данной публикации можно считать выделение моделей и дальнейшее расширение методов интервальной кинетики без каких-либо противоречий с ранее полученными результатами. В области классификации групп интервальных моделей кинетики реакций нами были предложены следующие модели:
1) модели решения прямых задач химической кинетики в форме дифференциальных уравнений при наличии информации об областях неопределенности кинетических параметров;
2) модели построения областей неопределенности кинетических параметров по данным физико-химического эксперимента (обратные задачи химической кинетики);
3) модели управления химическими реакциями при наличии информации об областях неопределенности кинетических параметров реакций;
4) синтетические модели, построенные на основе первых трех групп.
Подобная классификация охватывает такие вопросы исследований в кинетике химических реакций как: идентификацию параметров моделей, прогнозирование хода реакций и управление реакциями.
Ниже рассмотрим вопросы одновременного определения кинетических характеристик обратимых реакций первого порядка с использованием методики взвешенных эллипсоидов неопределенности (ВЭН)
[6].Постановка прямой и обратной задач химической кинетики для обратимых реакций первого порядка
Пусть А ![]() В (1)
В (1)
есть стехиометрическое уравнение обратимой реакции первого порядка в общем виде, где обе стадии - реакции первого порядка. В уравнении (1): А - исходное вещество; В - продукт прямой реакции первого порядка; стехиометрические коэффициенты a и b равны единице. Пусть k1 и k2 - константы скорости прямой и обратной реакций из (1) соответственно. Тогда выражение для скорости реакции (1) запишем следующим образом [10]:
![]() (2)
(2)
где [A](t) - концентрация вещества A в момент времени t (или обозначим проще: [A]); [B](t) - концентрация вещества B в момент времени t (или [B]).
В силу закона действующих масс для химической кинетики в любой момент времени t справедливы формулы:
![]() (3)
(3)
где ![]()
![]() - концентрации веществ А и
В в начальный момент времени t = 0 соответственно.
Подставляя (3) в (2), получим дифференциальное
уравнение:
- концентрации веществ А и
В в начальный момент времени t = 0 соответственно.
Подставляя (3) в (2), получим дифференциальное
уравнение:
![]() (4)
(4)
c начальным условием ![]() (5)
(5)
где ![]() -
концентрация вещества А в начальный момент
времени t = 0.
-
концентрация вещества А в начальный момент
времени t = 0.
Система (4), (5) есть задача Коши для
обыкновенных дифференциальных уравнений,
называемая прямой задачей химической кинетики в
случае определения концентраций веществ A и B по
известным начальным концентрациям ![]()
![]() и
константам скорости
и
константам скорости ![]() .
Выражение для равновесной концентрации вещества
А (при t ® ? ) запишем
в виде уравнения равновесного состояния:
.
Выражение для равновесной концентрации вещества
А (при t ® ? ) запишем
в виде уравнения равновесного состояния:
![]() , (6)
, (6)
где ![]() - равновесная
концентрация исходного вещества А в прямой
реакции обратимого процесса первого порядка.
- равновесная
концентрация исходного вещества А в прямой
реакции обратимого процесса первого порядка.
Используя формулу (6), уравнение (4) перепишем как:
![]() .(7)
.(7)
Из (7) следует соотношение:
![]() (8)
(8)
или ![]() . (9)
. (9)
Выражения (6) и (9) есть решение прямой задачи химической кинетики.
В обратной задаче химической кинетики
по известной сумме текущих концентраций веществ
A, B в моменты времени ti при ![]() , равновесной концентрации вещества
A или B необходимо определить константы скорости.
Формульная реализация этой задачи для обратимой
реакции первого порядка может быть представлена
следующим образом:
, равновесной концентрации вещества
A или B необходимо определить константы скорости.
Формульная реализация этой задачи для обратимой
реакции первого порядка может быть представлена
следующим образом:
![]() .
.
Интервальная постановка обратной
задачи химической кинетики для обратимой реакции первого порядка
При интервальной постановке обратной задачи химической кинетики для обратимой реакции первого порядка, решением которой будут интервальные оценки начальных концентраций веществ А, В и констант скоростей k1, k2, запишем выражения:
![]() ,
, ![]() , (10)
, (10)
где ![]() измеренные в моменты времени ti,
измеренные в моменты времени ti, ![]() концентрации вещества А;
концентрации вещества А; ![]() истинные значения
измеренных концентраций вещества А;
истинные значения
измеренных концентраций вещества А; ![]() верхняя граница абсолютной
погрешности измерений концентраций вещества А.
верхняя граница абсолютной
погрешности измерений концентраций вещества А.
Далее перепишем формулу (9) с учетом обозначений:
![]()
![]() , (11)
, (11)
![]() (12)
(12)
Oтсюда и из уравнений (10) следует
соотношение для множества неопределенности ![]() параметров a и b:
параметров a и b:
![]()
![]()
для ![]() , (13)
, (13)
где N - общее число рассматриваемых экспериментальных данных.
Введем новые переменные:
![]()
![]()
![]()
![]()
![]() для
для ![]() . (14)
. (14)
Тогда (13) можем записать в одной из эквивалентных форм:
![]()
для ![]() , (15)
, (15)
![]()
для ![]() . (16)
. (16)
Формулы (15), (16) означают, что задача
определения кинетических характеристик
обратимого процесса первого порядка ![]() сведена к задаче
определения параметров a и b линейной
функциональной зависимости
сведена к задаче
определения параметров a и b линейной
функциональной зависимости ![]() при точно известных значениях входных
переменных
при точно известных значениях входных
переменных ![]() и
измеренных с погрешностью
и
измеренных с погрешностью ![]() для
для ![]() выходных
переменных
выходных
переменных ![]() .
.
Поскольку натуральные логарифмы берем
только от положительных чисел, то погрешность
измерений ![]() должна
удовлетворять системе неравенств:
должна
удовлетворять системе неравенств:
![]() для
для ![]()
![]()
![]()
![]() (17)
(17)
Нижнее значение допустимой
погрешности ![]() обозначим
через
обозначим
через ![]() . Погрешность
. Погрешность ![]() находим из условий
непустоты множества W .
находим из условий
непустоты множества W .
Методика взвешенных эллипсоидов неопределенности при решении обратных интервальных задач оценивания
параметров линейных зависимостей
Наша задача заключается в погружении
множества неопределенности (15), (16) зависимости ![]() в эллипс
неопределенности (ЭН) вида:
в эллипс
неопределенности (ЭН) вида:
![]()
![]() (18)
(18)
Причем, ЭН будем искать как взвешенный эллипс неопределенности (ВЭН) метода наименьших квадратов (МНК):
![]()
![]() (19)
(19)
где ![]() - весовые
коэффициенты,
- весовые
коэффициенты, ![]() ,
удовлетворяющие условиям:
,
удовлетворяющие условиям:
![]()
![]()
![]() . (20)
. (20)
Исходя из (19), (20), можно заключить, что ![]() . Следовательно, задача
погружения множества неопределенности (15), (16) в
эллипс (19), (20) сведется к выбору по тем или иным
критериям чисел
. Следовательно, задача
погружения множества неопределенности (15), (16) в
эллипс (19), (20) сведется к выбору по тем или иным
критериям чисел ![]() при
при ![]() . В качестве такого
критерия возьмем площадь ЭН
. В качестве такого
критерия возьмем площадь ЭН ![]() . Центр эллипса (20) при известных
. Центр эллипса (20) при известных ![]() находим, решая
экстремальную задачу взвешенного МНК (ВМНК):
находим, решая
экстремальную задачу взвешенного МНК (ВМНК):
![]() (21)
(21)
Если условно считать числа ![]() для
для ![]() вероятностями появления в эксперименте
тройки чисел
вероятностями появления в эксперименте
тройки чисел ![]() , то можно
выписать следующие формулы для моментов первого,
второго порядков, дисперсий, ковариации и
коэффициента корреляции этих случайных величин:
, то можно
выписать следующие формулы для моментов первого,
второго порядков, дисперсий, ковариации и
коэффициента корреляции этих случайных величин:
![]()
![]()
![]()
![]() (22)
(22)
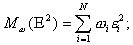
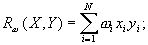 (23)
(23)
![]()
![]() (24)
(24)
![]()
![]() (25)
(25)
С помощью формул (22) - (25) и известных в математической статистике результатов ВМНК [11] получаем выражения для вычисления центра ЭН (19):
![]()
![]()
![]() (26)
(26)
Величины ![]()
![]() называют
среднеквадратическими отклонениями случайных
величин X и Y соответственно.
называют
среднеквадратическими отклонениями случайных
величин X и Y соответственно.
Согласно имеющимся выводам
математической статистики по оценке точности
ВМНК минимальное значение функции ![]() определяем по формуле:
определяем по формуле:
![]() , где
, где ![]() - центр ЭН. Отсюда площадь
ЭН
- центр ЭН. Отсюда площадь
ЭН ![]() рассчитываем:
рассчитываем:
![]()
![]() (27)
(27)
то есть выбираем оптимальные значения
параметров ![]() для
для ![]() из решения экстремальной
задачи
из решения экстремальной
задачи ![]() при условии (20).
при условии (20).
В случае двух измерений на основе
неравенства о среднем геометрическом и
арифметическом можно убедиться, что оптимальные
значения параметров ![]() и
соответствующий им центр эллипса находим
следующим образом:
и
соответствующий им центр эллипса находим
следующим образом:
![]()
![]()
![]() (28)
(28)
![]()
![]() (29)
(29)
Для получения формул рекуррентного перехода от n-го измерения к (n+1)-му предположим, что параметры эллипса (19) при
(n+1)-м измерении есть числа ![]()
![]() ,
определяемые из условия:
,
определяемые из условия:
![]()
![]() ,
,
![]() при
при ![]() (30)
(30)
В равенстве (30) числа ![]() при
при ![]() есть
параметры эллипса (19) при n измерениях. Наша цель -
подобрать такие
есть
параметры эллипса (19) при n измерениях. Наша цель -
подобрать такие ![]() , чтобы
площадь нового эллипса была минимальной.
, чтобы
площадь нового эллипса была минимальной.
Выразим величины уравнений (22) - (25)
через ![]() и вновь
поступающую информацию
и вновь
поступающую информацию ![]() тогда:
тогда:
![]()
![]() (31)
(31)
![]() при
при
![]() (32)
(32)
![]()
![]() (33)
(33)
![]()
![]() (34)
(34)
где ![]()
![]() (35)
(35)
Уравнение (27) принимает вид:
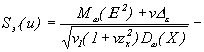
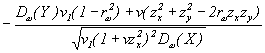
для ![]() , или
после некоторых преобразований:
, или
после некоторых преобразований:
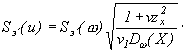
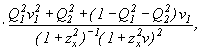
где ![]()
![]()
![]()
![]()
Проведем замену переменных ![]() отсюда
отсюда
![]()
![]()
Окончательное соотношение для поиска площади нового эллипса имеет вид:
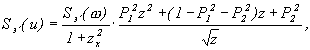 (36)
(36)
где 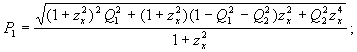
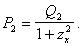
Далее нам необходимо найти z, при котором
![]() Для этого
сделаем следующую замену:
Для этого
сделаем следующую замену: ![]() и запишем
и запишем
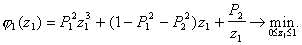
Найдем критические точки последней указанной функции из уравнения:
![]() или
или ![]() (37)
(37)
Положительный корень квадратного уравнения (37) равен:
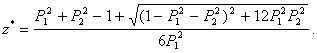 (38)
(38)
Необходимое и достаточное условие
принадлежности числа ![]() отрезку
[0;1] зададим соотношением:
отрезку
[0;1] зададим соотношением:
![]() (39)
(39)
Степень сокращения площади эллипса ![]() при поступлении нового
наблюдения находим как:
при поступлении нового
наблюдения находим как:
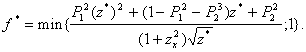 (40)
(40)
При ![]() множество неопределенности будет пустым.
множество неопределенности будет пустым.
На базе приведенных выше рассуждений
нетрудно построить рекуррентный алгоритм
погружения множества неопределенности W эмпирической зависимости ![]() в эллипс
неопределенности W 1.
в эллипс
неопределенности W 1.
Пример вычислений
В качестве примера выбрана обратимая реакция первого порядка превращения ?-оксимасляной кислоты в соответствующий лактон и воду [10]:
CH2OH-CH2-CH2-COOH![]() CH2-CH2-CH2-C=O+H2O
.
CH2-CH2-CH2-C=O+H2O
.
y – оксимасляная О
кислота лактон y - оксимасляной кислоты
В таблице 1 приведены исходные кинетические данные этой реакции.
Таблица 1
Исходные данные по кинетике превращения g - оксимасляной кислоты
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A(i), моль/л |
0.1582 |
0.1450 |
0.1324 |
0.1213 |
0.1115 |
0.1012 |
0.0923 |
0.0788 |
0.0668 |
ti, мин |
21 |
36 |
50 |
65 |
80 |
100 |
120 |
160 |
220 |
Кроме того, из опытов известно точное
значение равновесной концентрации y -
оксимасляной кислоты ![]() =0.0495
моль/л. В ходе проведения вычислительного
эксперимента величину оценки погрешности
измерений текущих концентраций контролируемого
вещества варьировали в широких пределах. В
таблице 2 выписали лишь несколько вариантов
расчетов.
=0.0495
моль/л. В ходе проведения вычислительного
эксперимента величину оценки погрешности
измерений текущих концентраций контролируемого
вещества варьировали в широких пределах. В
таблице 2 выписали лишь несколько вариантов
расчетов.
Результаты вычислений взвешенным
эллипсом неопределенности показали, что
критическими (предельными) погрешностями
измерений контролируемых концентраций
являются ![]() = 0.00052 и
= 0.00052 и
![]() = 0.01720. Ниже
= 0.01720. Ниже ![]() = 0.00052 множество
неопределенности параметров (a,b) пусто. А выше
= 0.00052 множество
неопределенности параметров (a,b) пусто. А выше ![]() = 0.01720 существует
естественное ограничение за счет
логарифмической функции.
= 0.01720 существует
естественное ограничение за счет
логарифмической функции.
Предлагаемые в таблице 2 результаты
расчетов показывают, что для нижнего значения
верхней оценки погрешности измерений ![]() (
(![]() =
0.00052) взвешенный эллипс неопределенности при n=9
стягивается в точку (S эл = 0.000000), и его
координаты можно считать оценкой параметров
линеаризованной зависимости. При этом укажем,
что для n=9 среднее значение параметра b=9.40
=
0.00052) взвешенный эллипс неопределенности при n=9
стягивается в точку (S эл = 0.000000), и его
координаты можно считать оценкой параметров
линеаризованной зависимости. При этом укажем,
что для n=9 среднее значение параметра b=9.40 ![]()
10 -3, параметр (-a ), полученный непосредственно из эксперимента, равен 2.01807. Параметру (-a ) соответствует значение начальной
концентрации ? -оксимасляной кислоты [A]0=0.18241 моль/л. То есть, в нашем случае, экспериментальный (как бы проверочный) результат практически совпадает с рассчитанным по методике взвешенного эллипса неопределенности. Отметим, что в таблице 2 введены следующие обозначения: а, b – параметры линеаризованной зависимости; Sэл - площадь ВЭН; f - степень сокращения ВЭН при поступлении нового измерения; ?i – рассчитанные веса для имеющихся экспериментальных данных (указаны в порядке возрастания количества измеренных точек от 1 до 9).
Таблица 2
Оценки кинетических параметров и параметров эллипса, вычисленные по
методике взвешенного эллипса неопределенности
![]() = 0.00052 (нижняя
граница
= 0.00052 (нижняя
граница ![]() )
)
i |
-a |
b |
Sэл |
f |
[A]0 |
2 |
2.03792 |
0.00863 |
0.00001 |
0.17980 |
|
3 |
2.02280 |
0.00923 |
0.000001 |
0.16943 |
0.18178 |
4 |
2.01950 |
0.00935 |
0.000001 |
0.72183 |
0.18222 |
5 |
2.01647 |
0.00945 |
0.000000 |
0.73498 |
0.18262 |
6 |
2.01647 |
0.00945 |
0.000000 |
1.00000 |
0.18262 |
7 |
2.01647 |
0.00945 |
0.000000 |
1.00000 |
0.18262 |
8 |
2.01647 |
0.00945 |
0.000000 |
1.00000 |
0.18262 |
9 |
2.01807 |
0.00940 |
0.000000 |
1.00000 |
0.18241 |
Продолжение таблицы 2
i |
w i |
||||||||
0.56437 |
0.43563 |
||||||||
3 |
0.44663 |
0.34474 |
0.20863 |
||||||
4 |
0.41807 |
0.32270 |
0.19529 |
0.06394 |
|||||
5 |
0.39842 |
0.30753 |
0.18611 |
0.06094 |
0.04700 |
||||
6 |
0.39842 |
0.30753 |
0.18611 |
0.06094 |
0.04700 |
0.00000 |
|||
7 |
0.39842 |
0.30753 |
0.18611 |
0.06094 |
0.04700 |
0.00000 |
0.00000 |
||
8 |
0.39842 |
0.30753 |
0.18611 |
0.06094 |
0.04700 |
0.00000 |
0.00000 |
0.00000 |
|
9 |
0.39753 |
0.30684 |
0.18569 |
0.06080 |
0.04689 |
0.00000 |
0.00000 |
0.00000 |
0.00225 |
Продолжение таблицы 2
![]() = 0.01720 (верхняя
граница
= 0.01720 (верхняя
граница ![]() )
)
i |
-a |
b |
Sэл |
f |
[A]0 |
2 |
2.04526 |
0.00889 |
0.01217 |
0.17885 |
|
3 |
2.02660 |
0.00963 |
0.008720 |
0.30332 |
0.18128 |
4 |
2.02035 |
0.00984 |
0.007466 |
0.48353 |
0.18211 |
5 |
2.01516 |
0.00999 |
0.006968 |
0.64128 |
0.18280 |
6 |
2.01314 |
0.01004 |
0.006622 |
0.68891 |
0.18307 |
7 |
2.00995 |
0.01012 |
0.006540 |
0.84338 |
0.18350 |
8 |
2.00995 |
0.01012 |
0.006540 |
1.00000 |
0.18350 |
9 |
2.00995 |
0.01012 |
0.006540 |
1.00000 |
0.18350 |
Продолжение таблицы 2
i |
w i |
||||||||
2 |
0.56562 |
0.43438 |
|||||||
3 |
0.38949 |
0.29912 |
0.31139 |
||||||
4 |
0.30174 |
0.23173 |
0.24124 |
0.22529 |
|||||
5 |
0.25691 |
0.19730 |
0.20540 |
0.19181 |
0.14858 |
||||
6 |
0.22964 |
0.17636 |
0.18359 |
0.17145 |
0.13281 |
0.10615 |
|||
7 |
0.21949 |
0.16856 |
0.17548 |
0.16387 |
0.12693 |
0.10145 |
0.04422 |
||
8 |
0.21949 |
0.16856 |
0.17548 |
0.16387 |
0.12693 |
0.10145 |
0.04422 |
0.00000 |
|
9 |
0.21949 |
0.16856 |
0.17548 |
0.16387 |
0.12693 |
0.10145 |
0.04422 |
0.00000 |
0.00000 |
Выводы
1. Предложена классификация групп интервальных моделей кинетики химических реакций.
2. В качестве одной из вычислительных методик функционирования интервальных моделей рассмотрена методика взвешенного эллипсоида неопределенности.
3. Построен рекуррентный алгоритм определения параметров зависимостей, сводящихся к линейным, по методике ВЭН.
4. На примере известной из литературы [10] обратимой реакции первого порядка показано, что методика ВЭН с достаточной степенью точности описывает экспериментальные данные и позволяет одновременно оценивать несколько кинетических характеристик химической реакции (в нашем случае это: начальная концентрация реагента и сумма констант скорости обратимого процесса). Последнее является очень важной и на практике мало и трудно решаемой задачей (например, для целей кинетических методов анализа).
СПИСОК ЛИТЕРАТУРЫ
1. Белов В.М. // Изв. вузов. Химия и хим. технол.. 1997. Т. 40. N 5. С. 17-20.2. Белов В.М., Королькова С.М. // Изв. вузов. Химия и хим. технол.. 1997. Т. 40. N 6. С. 135-136.
3. Белов В.М., Евстигнеев В.В., Карбаинов Ю.А., Суханов В.А. // Изв. вузов. Химия и хим. технол.. 1997. Т. 40. N 6. С. 136-137.
4. Белов В.М., Суханов В.А., Лагуткина Е.В. // Вычислительные технологии. 1997. Т. 2. N 1. С. 10- 18.
5. Белов В.М. и др. // Химия растительного сырья. 1997. N 3. С. 26-30.
6. Белов В.М., Суханов В.А., Унгер Ф.Г. Теоретические и прикладные аспекты метода центра неопределенности. Новосибирск: Наука, 1995. 144 с.
7. Спивак С.И. Информативность эксперимента и проблема неединственности решения обратных задач химической кинетики: Автореф. дис. докт. наук. Черноголовка, 1984. 30 с.
8. Быков В.И., Добронец Б.С. // Математические проблемы химической кинетики. Новосибирск: Наука, 1989. С. 226-232.
9. Круглов А.В., Спивак С.И. // Математические методы в химической кинетике. Новосибирск: Наука, 1990. С. 152-156.
10. Эмануэль Н.М., Кнорре Д.Г. Курс химической кинетики. М.: Высш. шк., 1984. 463 с.
11. Доерфель К. Статистика в аналитической химии. М.: Мир, 1969. 347 с.