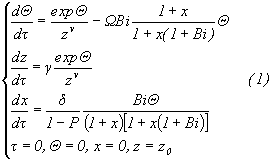
Основы моделирования процесса взаимодействия одиночной частицы с плавящейся средой при наличии тепловыделения от образования интерметаллидных соединений
В. В. Евстигнеев, С. В. Краснощеков, В. Ю. Филимонов
В последнее время, многими авторами ( см. например [1]) подчеркивалось, что СВC в режиме теплового взрыва обладает определенными преимуществами по сравнению с фронтальным режимом синтеза. Вместе с тем закономерности макрокинетики разогрева гетерогенных конденсированных систем в режиме теплового взрыва изучены недостаточно полно, при этом как правило акцент в теоретических или экспериментальных работах на указанную тему сделан на исследовании кинетики фазообразования и состава конечного продукта в зависимости от параметров синтеза [1], [2]. С другой стороны возникает проблема создания быстродействующих и экономичных СВС реакторов для получения продукта требуемого состава и свойств. Последнее невозможно без четкого понимания теплофизической обстановки процесса, определяющей тепловую активность шихты и дающей возможность управлять процессом синтеза. Особенностью взаимодействия гетерогенных конденсированных систем является с одной стороны сильная зависимость кинетики разогрева и свойств продукта от структурных характеристик исходной шихты (размера частиц порошков, соотношения объемов компонентов, пористости, удельной поверхности и т. д.), с другой наличие фазового превращения в процессе синтеза. В связи с этим возникает необходимость исследования влияния теплоотвода на фазовый переход в процессе взаимодействия в режиме теплового взрыва для определенных исходных структур. Наиболее специфичной в этом отношении, является ситуация, когда объем легкоплавкого компонента в шихте в несколько раз превосходит объем тугоплавкого. Естественно, что при хорошем перемешивании шихты, если размеры частиц легкоплавкого и тугоплавкого компонентов сопоставимы, контакт тугоплавких частиц маловероятен. В случае мелких легкоплавких и крупных тугоплавких, как показано в [3], последние в любом случае окружены расплавом, следовательно, на начальном этапе разогрева весь теплоотвод будет сконцентрирован внутри системы, вплоть до заполнения ячейки расплавом. Лишь только после этого можно говорить о ньютоновском теплоотводе через поверхность образца, рассмотренном в [1]. В этом случае, величина разогрева до момента заполнения ячейки будет являться функцией теплофизических параметров задачи и величины размера ячейки, т. е. не будет произвольной. Вследствие этого возникает необходимость анализа уравнений теплового баланса на уровне элементарной ячейки плавления при наличии специфического теплоотвода на фазовый переход, поскольку не ясно когда плавление предшествует разогреву, когда разогрев происходит быстрее плавления, когда эти процессы идут с одинаковой интенсивностью. Таким образом, вопрос требует количественного исследования.
Результаты анализа
В настоящей работе анализируется этап, характеризуемый внутренним теплоотводом, с точки зрения критических условий саморазогрева для неограниченной ячейки. Взаимодействие происходит с плавящейся пористой средой при наличии тепловыделения от поверхности частицы в расплав при слабом кинетическом торможении реакции. Соответствующая система уравнений (в предположении b =RT0/E<<1) в обезразмеренной форме будет иметь вид:
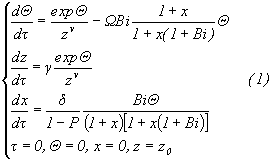
где 
, 
, 
, 
, 
, 
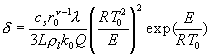. Индексы “l” - относим к
легкоплавкому компоненту, ''s'' - к тугоплавкому.
Здесь
- глубина плавления, y -
радиус фронта плавления, h - толщина пленки
продукта, l
- теплопроводность жидкой фазы, P - пористость, L -
удельная теплота плавления, Q, E - удельный
тепловой эффект на единицу массы легкоплавкого
компонента и энергия активации соответственно, 
.
Последнее уравнение системы (1) получено в результате решения задачи о движении сферического фронта плавления в квазистационарном приближении [4].
Постановка задачи в форме (1)
правомочна для случая, когда мелкие (по сравнению
с тугоплавкими) частицы легкоплавкого
компонента образуют жесткий каркас, массообмен
между конденсированной и газовой фазой
отсутствует (безгазовое горение), температуры
конденсированной и газовой фазы одинаковы.
Последнее имеет место, если время тепловой
релаксации газовой фазы, 
значительно меньше характерного времени
разогрева частицы 
, т. е.
, где
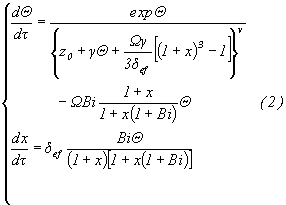
где
d ef=d /(1-P). Для анализа устойчивости (2) применим метод изоклин dQ /dt =0 (демаркационная кривая) [5]. Вначале рассмотрим линейный закон торможения n =0. Из (1) следует, что при Bi<<1 решение задачи классическое [6] и W Bi=e, Q =1 - критические условия для одиночной частицы при постоянной температуре среды. При конечных Bi, значение эффективного коэффициента теплоотдачи (функции стоящей множителем перед Q в первом уравнении) меньше чем W Bi, т. е. наличие плавящейся среды смягчает условия воспламенения. Из уравнения изоклины dQ /dt =0 получим:
где
W ef=W Bi. Заметим, что условие
, или W ef <e является тривиальным и его
выполнение гарантирует воспламенение одиночной
частицы ("отрыв"). В случае W ef >e необходимо
рассмотреть две ситуации:
1) 
имеет два
корня (
)
2) не имеет
корней (
).
Оба случая изображены на рисунке 1.
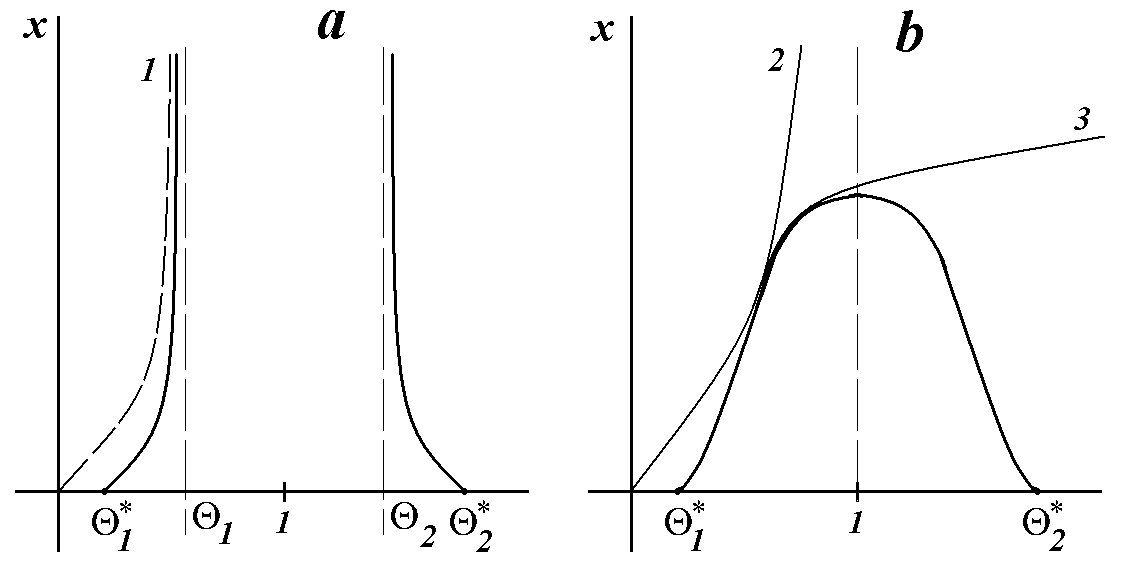Рис. 1. Изоклина dQ /dt =0, 1) 
, 2) 
. Кривая 1 - ход фазовой траектории,
кривые 2, 3 - фазовые траектории в
околокритической области, Q 1*, Q 2* - корни уравнения 
.
В обоих случаях фазовая траектория не
пересечет изоклину. В случае a, траектория будет
асимптотически сближаться с изоклиной
экстремумов. В случае b - Q =1 - критическая
асимптота при 
. Особый
интерес представляет анализ областей
устойчивости на параметрической плоскости W -d .
Для этого получим приближенный вид фазовой
траектории x(Q ) исходя из естественного условия
Bi® 0, x® 0 (отсутствие теплового контакта
частица-расплав). Тогда представим x(Q ) в виде
формального разложения при малых Bi:
Подставив (4) в уравнение фазовой траектории, dx/d
Q , после несложных преобразований получим в первом приближении:
Подставив (5) в (3), выразив
W ef через d и положив Q =Q cr=1, найдем:
Зависимость (6) при разных Bi изображена на рисунке 2 пунктирной кривой.
Для кривой 3, область I - подкритическая область (слияние), область II - режим разогрева с плавлением, область III - режим отрыва.
Далее перейдем к выяснению влияния кинетического торможения на критические условия,
n =1. Уравнение для изоклины dQ /dt =0 значительно усложнится. Положив z0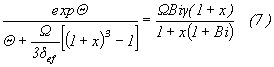=0, получим
Найдем уравнение огибающей экстремумов
демаркационной кривой (7). Для этого
продифференцируем (7) по x и используем условие dQ /dx=0. Получим:
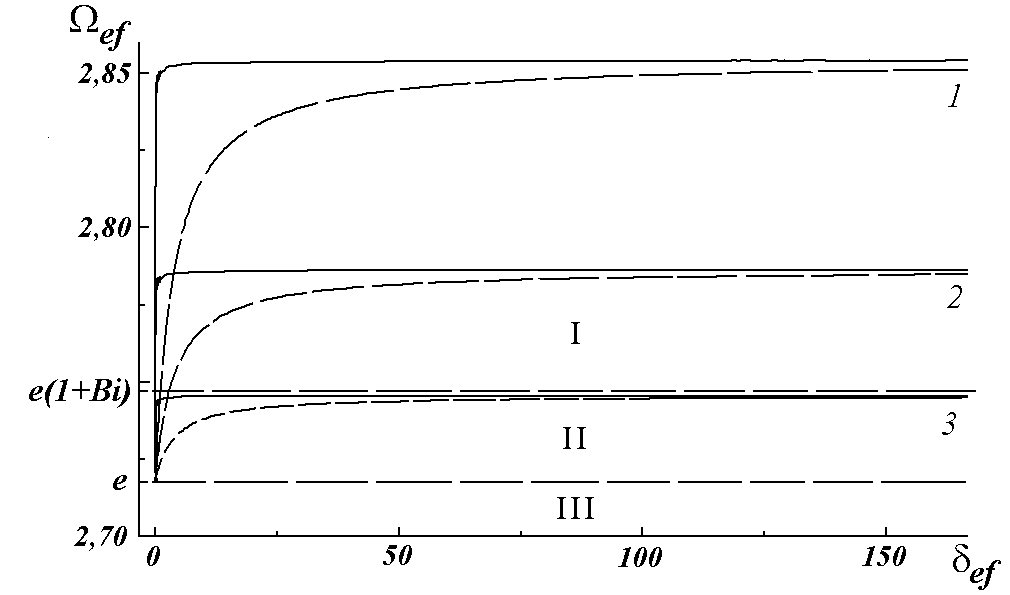
Рис. 2. Зависимость
W ef(d ef) для критических условий. Пунктир - расчет по (6), сплошная кривая - численный анализ. 1. Bi=0,05, 2. Bi=0,025, 3. Bi=0,01.
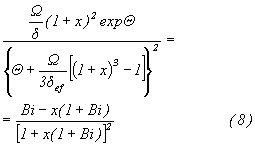
С использованием (7), определим:
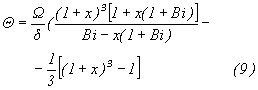
На рисунке 3 изображена зависимость (9) при Bi=1.
Из рисунка видно, что точкой срыва фазовой траектории является точка a [5]. Для случая кривой 2, критические условия гарантированно не выполняются. В этом случае, как следует из анализа (7), при x=0,
W Big >e2/4. Кривая 1, W Big <e2/4. Таким образом критические условия при наличии кинетического торможения определяются срывом максимума на фазовой траектории. На рисунке 4, изображен ход фазовой траектории в околокритической области.Для получения диаграммы критических параметров, необходимо решить уравнения (7), (8) совместно с уравнением фазовой траектории. На рисунке 5 изображены результаты численного анализа критической кривой
W efg =f(d ef g ).Точка A соответствует критическому условию, полученному в задаче [7] для одиночной частицы, окисляющейся по параболическому закону. Как видно из рисунка, диаграмма качественно ничем не отличается от ситуации линейного закона торможения, но в данном случае необходимо учитывать наличие параметра
g , характеризующего торможение слоем продукта реакции. Рост последнего приводит к "сжатию" надкритической области на диаграмме.
ВЫВОДЫ
Результаты данной работы позволяют сделать вывод, что критерий воспламенения
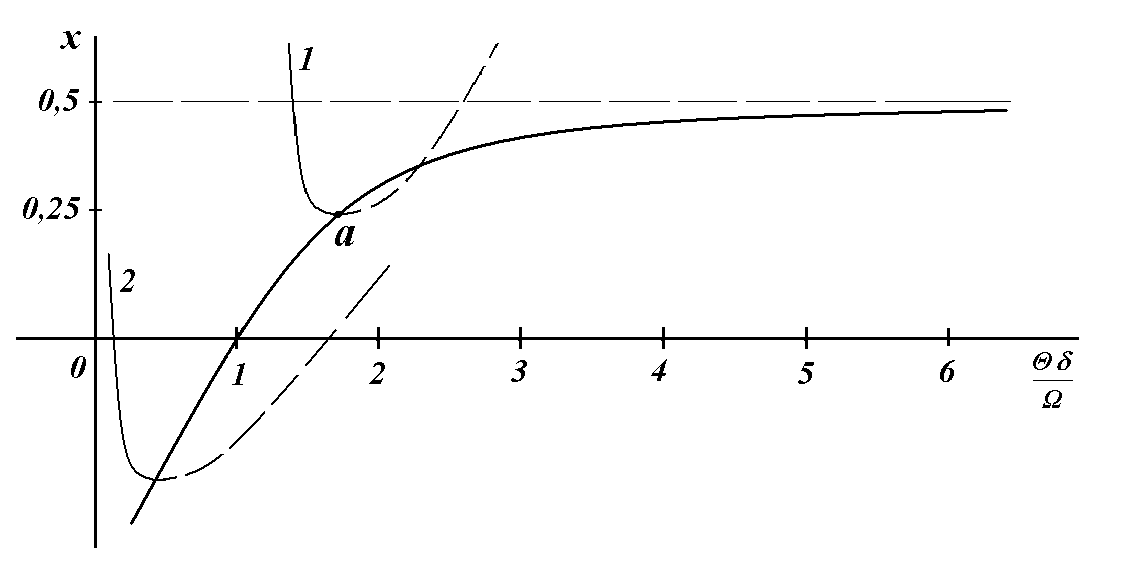
Рис. 3. Изоклина экстремумов демаркационной кривой при Bi=1. Кривая 1 -
W Big <e2/4, кривая 2 - W Big >e2/4. Пунктир - неустойчивая ветвь.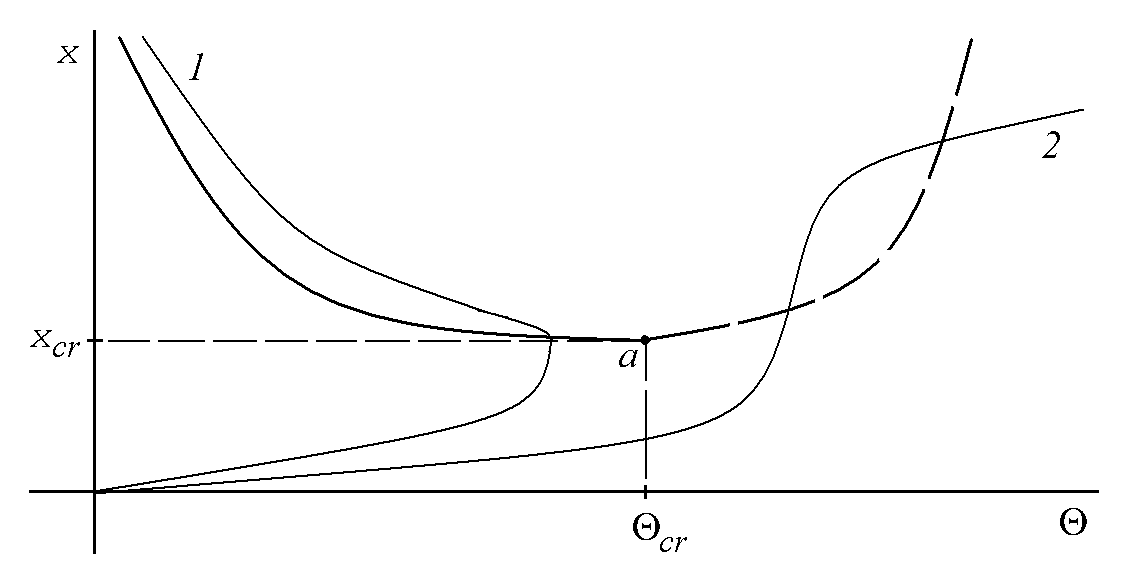
Рис. 4. Поведение фазовой траектории при околокритических значениях параметров. Кривая 1 - докритическая, 2 - надкритическая.
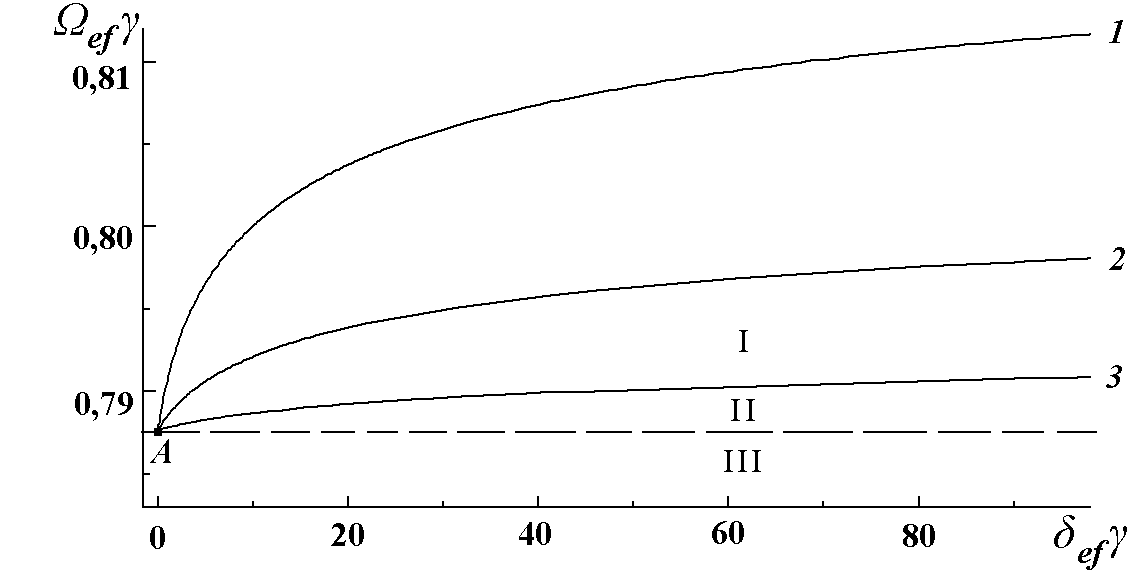
Рис. 5. Диаграмма критических параметров. 1. Bi=0,05, 2. Bi=0,025, 3. Bi=0,01, при
g =0,1.
частицы, находящейся в контакте с плавящейся средой, в существенной степени зависит от качества теплового контакта частица-расплав, т. е. от критерия Био. В случае Bi<<1, критические условия самовоспламенения мало отличаются от условий воспламенения одиночной частицы в среде с постоянной температурой. В случае если они выполнены, реализуется режим "отрыва". Если Bi>1 критические условия соответствуют саморазогреву с плавлением (при разогреве частицы "тянут" за собой расплав). Если критические условия не выполнены, реализуется режим слияния, когда тепло от реакции выделившееся на поверхности частицы полностью уходит на плавление и разогревы не велики. В рассмотренной задаче, варьируемыми (внешними) параметрами является размер частицы и пористость для заданной бинарной системы. С изменением последних появляется возможность перехода из надкритической области в подкритическую и наоборот.
Из вышеизложенного следует, что вводить в рассмотрение макротепловой баланс образца как целого, можно только после окончания плавления легкоплавкого компонента с учетом соответствующих начальных условий, зависящих как от свойств плавящейся среды, так и от параметров диффузии и теплового контакта.
Литература
1. Лапшин О. В., Овчаренко В. Е. Математическая модель высокотемпературного синтеза алюминида никеля Ni3Al в режиме теплового взрыва порошковой смеси чистых элементов. // Физика горения и взрыва. 1996, т. 32, N3, с. 68-76.
2. Смоляков В. К., Некрасов Е. А. Максимов Ю. Н. Моделирование безгазового горения с фазовыми превращениями. // Физика горения и взрыва. 1984, т. 20, N2, с. 63-73.
3. Кирдяшкин А. И., Лепакова О. К. и др. Структурные превращения компонентов порошковой смеси в волне безгазового горения. // Физика горения и взрыва. 1989, т. 25, N6, с. 67-72.
4. Некрасов Е. А., Тимохин А. М., Пак А. Т. К теории безгазового горения с фазовыми превращениями. // Физика горения и взрыва. 1990, т. 26, N5, с. 79-85.
5. Бабушок В. И., Гольдштейн В. М., Романов А. С., Бабкин В. С. Тепловое воспламенение в инертной пористой среде. // Физика горения и взрыва. 1992, т. 28, N4, С. 3-10.
6. Франк-Каменецкий Д. А. Диффузия и теплопередача в химической кинетике. М.:Наука, 1987.
7. Розенбанд В. И., Черненко Е. Ф. Расчет нижнего концентрационного предела самовоспламенения газовзвеси и слоя порошка металла // Физика горения и взрыва. 1982, т. 18, N3, С. 9-17.