НОВЫЙ ПОДХОД К ПРОБЛЕМЕ МОДЕЛИРОВАНИЯ СГОРАНИЯ СМЕСИ В ДВС С ИСКРОВЫМ ЗАЖИГАНИЕМ
Д.Д. Матиевский, П.К. Сеначин, М.Ю. Свердлов, М.А. Ильина
Горение горючих смесей в закрытых сосудах и двигателях внутреннего сгорания с искровым зажиганием обычно происходит за счет распространения пламени по объему системы (волны дефлаграции), даже если пламя турбулизированно. При этом динамика сгорания (скорость выгорания смеси) и динамика давления в системе существенным образом зависят от закона изменения поверхности пламени. Форма и поверхность пламени при сгорании гомогенных горючих смесей в закрытых сосудах и двигателях существенно влияют на основные черты динамики процесса: скорость превращения вещества, скорость нарастания давления, распределение скоростей газа и т.д. В связи с этим исследование общих свойств и особенностей динамики сгорания газа при разных законах изменения поверхности пламени представляет теоретический и практический интерес.
В двигателях внутреннего сгорания динамика процесса обычно описывается различными полуэмпирическими уравнениями выгорания смеси, основанными на объемном законе выгорания [1-3]. Эти уравнения не учитывают двухзонность реального процесса сгорания в двигателе. Двухзонные модели сгорания, учитывающие реальную геометрию пламени в сферических сечениях камеры сгорания, гораздо сложнее и применяются в кинетических и динамических задачах процессов горения сравнения недавно [4-6].
В настоящей работе было проведено исследование влияния геометрии камеры сгорания на динамику сгорания смеси ДВС с точечным искровым зажиганием. Рассмотрены случаи, учитывающие реальную геометрию пламени в сферических сечениях камер сгорания цилиндрической формы с точкой зажигания на оси (Модель 1, рис. 1а) , симметричной камеры со смещенной точкой зажигания ( Модель 1А, рис. 1б) и клиновидной камеры с асимметричным зажиганием - (Модель 7, рис. 1в). Полагаем, что эти модели являются предельными (или близкими к ним) как в отношении геометрии камеры сгорания, так и расположения точки зажигания.
Постановка задачи
Предполагается, что несмотря на турбулентный характер горения распространяющееся пламя тонкое, то есть размер камеры велик по сравнению с шириной зоны пламени. Процесс горения адиабатический и медленный, поэтому давление одинаково во всех точках камеры сгорания и изменяется только во времени. Как обычно, основными независимыми геометрическими параметрами двигателя полагаем радиус кривошипа ![]() , диаметр поршня
, диаметр поршня ![]() и геометрическую степень сжатия
и геометрическую степень сжатия ![]() . В качестве независимой переменной, аналогичной времени, примем угол поворота коленчатого вала
. В качестве независимой переменной, аналогичной времени, примем угол поворота коленчатого вала ![]() . Параметры смеси в момент зажигания, соответствующий углу поворота коленчатого вала
. Параметры смеси в момент зажигания, соответствующий углу поворота коленчатого вала ![]() , предполагаются известными.
, предполагаются известными.
Рабочий объем системы определяется известной в динамике двигателей приближенной формулой для аксиального механизма [7]:
![]() .
.
Система, описывающая процесс горения смеси, включает уравнения:
динамики давления (энергии всей системы)
![]() , (1)
, (1)
динамики объема системы (и его интеграл)
![]() , (2)
, (2)
![]() ,
,
энергии смеси перед фронтом пламени (и его интеграл)
![]() , (3)
, (3)
![]() ,
,
состояния смеси перед фронтом пламени
![]() , (4)
, (4)
объема продуктов горения
![]() , (5)
, (5)
массовой скорости горения
![]() (6)
(6)
и зависимости нормальной скорости пламени от давления и температуры
![]() . (7)
. (7)
|
а) |
|
|
б) |
|
|
в) |
|
|
Рис. 1. Распространение фронта пламени в камере сгорания двигателя с искровым зажиганием: rf- радиус сферического фронта пламени; |
|
В систему уравнений (1-7) входят:
безразмерные переменные
![]() - давление,
- давление,
![]() - температура,
- температура,
![]() - объем,
- объем,
![]() - массовая доля продуктов горения,
- массовая доля продуктов горения,
![]() - нормальная скорость пламени;
- нормальная скорость пламени;
параметры процесса
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
постоянные
![]() - универсальная газовая постоянная;
- универсальная газовая постоянная;
![]() - мольные теплоемкости;
- мольные теплоемкости;
![]() - тепловой эффект химической реакции (на моль горючего компонента) и удельная энтальпия сгорания топлива;
- тепловой эффект химической реакции (на моль горючего компонента) и удельная энтальпия сгорания топлива;
![]() - масса топлива, поступающего в камеру сгорания за один цикл, и его мольная стехиометрическая и действительная доли;
- масса топлива, поступающего в камеру сгорания за один цикл, и его мольная стехиометрическая и действительная доли;
![]() - коэффициент избытка воздуха;
- коэффициент избытка воздуха;
![]() - порядок химической реакции;
- порядок химической реакции;
![]() - “нормальная" скорость турбулентного пламени;
- “нормальная" скорость турбулентного пламени;
![]() - текущая нормальная скорость пламени;
- текущая нормальная скорость пламени;
![]() - фактор турбулизации пламени [8-10];
- фактор турбулизации пламени [8-10];
![]() - скорость турбулентного переноса;
- скорость турбулентного переноса;
![]() - нормальная скорость пламени для смеси стехиометрического состава в момент зажигания;
- нормальная скорость пламени для смеси стехиометрического состава в момент зажигания;
![]() - частота вращения коленчатого вала;
- частота вращения коленчатого вала;
![]() - отношение радиуса кривошипа к длине шатуна;
- отношение радиуса кривошипа к длине шатуна;
![]() - диаметр поршня, объемы камеры сгорания и цилиндра.
- диаметр поршня, объемы камеры сгорания и цилиндра.
Индексы ![]() относятся к моменту зажигания смеси, свежей смеси и продуктам горения соответственно.
относятся к моменту зажигания смеси, свежей смеси и продуктам горения соответственно.
Математическая модель
Модель 1
Для модели с симметричной камерой
сгорания цилиндрической формы с точкой зажигания на оси (Модель 1, рис. 1а) объем и высота камеры сгорания равны
![]() ,
,
![]() . (8)
. (8)
Функция относительной площади поверхности пламени, входящая в систему уравнений (1-7), определяется отношением
![]() , (9)
, (9)
где ![]() - функция площади поверхности активного пламени, зависящая от формы камеры сгорания.
- функция площади поверхности активного пламени, зависящая от формы камеры сгорания.
Для Модели 1 функция относительной площади поверхности активного пламени ![]() в зависимости от текущих значений координаты поршня
в зависимости от текущих значений координаты поршня ![]() и объема продуктов горения
и объема продуктов горения ![]() находится из уравнений:
находится из уравнений:
при ![]() ,
, ![]() (10)
(10)
![]() ,
, ![]() ;
;
при ![]() ,
, ![]() (11)
(11)
![]() ,
, ![]() ;
;
при ![]() ,
, ![]() (12)
(12)
![]() ,
,
![]() ,
,
при ![]() ,
, ![]() (13)
(13)
![]() ,
,
![]()
![]() .
.
Отметим, что в уравнениях (12) и (13) радиус фронта пламени ![]() является неявной функцией
является неявной функцией ![]() и
и ![]() и определяется численным решением уравнения методом дихотомии.
и определяется численным решением уравнения методом дихотомии.
Модель 1А
Для модели с симметричной камерой сгорания цилиндрической формы со смещенной точкой зажигания ( Модель 1А, рис. 1б) объем и высота камеры сгорания равны соответствующим параметрам для Модели 1 и определяются уравнениями (8). Функция относительной площади поверхности пламени ![]() определяется отношением (9).
определяется отношением (9).
В сферических сечениях камеры сгорания поверхностью пламени с радиусом ![]() в зависимости от координаты поршня
в зависимости от координаты поршня ![]() , как и прежде, можно выделить четыре различных ситуации. Для Модели 1А функция площади поверхности активного пламени в зависимости от текущих значений координаты поршня
, как и прежде, можно выделить четыре различных ситуации. Для Модели 1А функция площади поверхности активного пламени в зависимости от текущих значений координаты поршня ![]() и объема продуктов горения
и объема продуктов горения ![]() определяется из уравнений:
определяется из уравнений:
при ![]() ,
, ![]() (14)
(14)
![]() ,
,
![]()
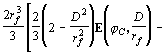
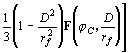 ;
;
при ![]() , (15)
, (15)
![]()
![]() ,
,
![]()
![]()
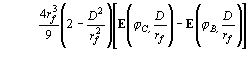 ;
;
при ![]() (16)
(16)
![]() ,
,
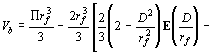
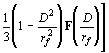 ;
;
при ![]() ,
, ![]() (17)
(17)
![]() ,
,
![]()
![]()
![]()
![]() .
.
В уравнениях (14-17) обозначено:
![]() ,
,![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , (17ў )
, (17ў )
где ![]() ,
, ![]() - неполный и полный эллиптические интегралы 1-го рода (с модулем
- неполный и полный эллиптические интегралы 1-го рода (с модулем ![]() ) в нормальной форме Лежандра;
) в нормальной форме Лежандра; ![]() ,
, ![]() - неполный и полный эллиптические интегралы 2-го рода (с модулем
- неполный и полный эллиптические интегралы 2-го рода (с модулем ![]() ) в нормальной форме Лежандра.
) в нормальной форме Лежандра.
Модель 7
Для клиновидной камеры сгорания с асимметричным зажиганием (Модель 7, рис. 1в) объем и высота камеры сгорания равны
![]() ,
,
![]() ,
,
поэтому высота камеры ![]() также не зависит от диаметра поршня и оказывается в два раза больше, чем в Модели 1 и Модели 1А. Аналогично в сферических сечениях камеры сгорания поверхностью пламени с радиусом
также не зависит от диаметра поршня и оказывается в два раза больше, чем в Модели 1 и Модели 1А. Аналогично в сферических сечениях камеры сгорания поверхностью пламени с радиусом ![]() в зависимости от координаты поршня
в зависимости от координаты поршня ![]() , как и прежде, можно выделить четыре различных ситуации. Для Модели 7 функция площади пламени
, как и прежде, можно выделить четыре различных ситуации. Для Модели 7 функция площади пламени ![]() в зависимости от текущих значений координаты поршня
в зависимости от текущих значений координаты поршня ![]() и объема продуктов горения
и объема продуктов горения ![]() определяется из уравнений:
определяется из уравнений:
при ![]() ,
, ![]() (18)
(18)
![]()
![]()
![]() ,
,
![]()
![]()
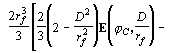
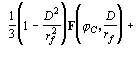
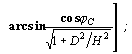
при ![]() (19)
(19)
![]()
 ,
,
![]()
![]()
![]()
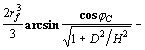
![]()
![]() ;
;
при ![]() (20)
(20)
![]() ,
,
![]()
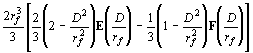 ;
;
при ![]() ,
, ![]() (21)
(21)
![]() ,
,
![]()
![]()
![]()
![]() .
.
В уравнениях (18 - 21) обозначено:
![]() ,
, ![]() ,
,
![]() ;
;
![]() ,
, ![]() ,
, ![]() ,
, ![]() - неполный и полный эллиптические интегралы 1-го рода и 2-го рода (с модулем
- неполный и полный эллиптические интегралы 1-го рода и 2-го рода (с модулем ![]() ) в нормальной форме Лежандра (17ў ). Хотя эти интегралы табулированы [12,13}, однако в практических расчетах удобнее их рассчитывать численно, например, методом прогонки (используя 3 или 4 - точечную интерполяцию) [14, 15].
) в нормальной форме Лежандра (17ў ). Хотя эти интегралы табулированы [12,13}, однако в практических расчетах удобнее их рассчитывать численно, например, методом прогонки (используя 3 или 4 - точечную интерполяцию) [14, 15].
Результаты расчетов и обсуждение
Система уравнений (1-7) решалась численно методом Рунге-Кутта 4-го порядка с переменным шагом интегрирования при различных углах зажигания ![]() (от -30 до 0 Град. п.к.в.), степени сжатия
(от -30 до 0 Град. п.к.в.), степени сжатия ![]() (от 7 до 10) и частоты вращения коленчатого вала
(от 7 до 10) и частоты вращения коленчатого вала ![]() (от 2000 до 6000 об/мин) для трех геометрий камер сгорания по уравнениям (10)-(13) для Модели 1 , (14)-(17) для Модели 1А и (18)-(21) для Модели 7.
(от 2000 до 6000 об/мин) для трех геометрий камер сгорания по уравнениям (10)-(13) для Модели 1 , (14)-(17) для Модели 1А и (18)-(21) для Модели 7.
Некоторые результаты интегрирования системы уравнений (1-7) представлены на рис. 2-8, в виде зависимости давления в камере сгорания ![]() от угла поворота коленчатого вала
от угла поворота коленчатого вала ![]() при трех значениях угла зажигания
при трех значениях угла зажигания ![]() . Для расчетов был взят двигатель М-408. В качестве топлива выбран гептан
. Для расчетов был взят двигатель М-408. В качестве топлива выбран гептан ![]() . Его низшая теплота сгорания 4480 КДж/моль [11]. Мольная стехиометрическая доля топлива, поступающего в камеру сгорания за один цикл,
. Его низшая теплота сгорания 4480 КДж/моль [11]. Мольная стехиометрическая доля топлива, поступающего в камеру сгорания за один цикл, ![]() найдена при горении гептана в воздухе средней влажности. Исходные данные для расчетов приведены в таблице 1.
найдена при горении гептана в воздухе средней влажности. Исходные данные для расчетов приведены в таблице 1.
Проведенные расчеты показывают влияние степени сжатия на динамику процесса. Из рис.2-4 видно, что увеличение степени сжатия ![]() от 7 до 10 практически не оказывает влияние на длительность процесса сгорания. При этом индикаторная диаграмма для всех типов камер сгорания смещается по вертикали, т.е. с увеличением степени сжатия растут максимальное давление в цилиндре и давление конца сгорания.
от 7 до 10 практически не оказывает влияние на длительность процесса сгорания. При этом индикаторная диаграмма для всех типов камер сгорания смещается по вертикали, т.е. с увеличением степени сжатия растут максимальное давление в цилиндре и давление конца сгорания.
На рис.2-7 приведены индикаторные диаграммы, показывающие изменение давления в камере сгорания в зависимости от
угла опережения зажигания ![]() . Вначале процесс сгорания смещается по линии расширения, далее индикаторные диаграммы резко меняются, что соответствует реальному циклу. Из рисунков также видно, что с ростом
. Вначале процесс сгорания смещается по линии расширения, далее индикаторные диаграммы резко меняются, что соответствует реальному циклу. Из рисунков также видно, что с ростом ![]() растет максимальное индикаторное давление , что наблюдается и в действительности.
растет максимальное индикаторное давление , что наблюдается и в действительности.
Таблица 1
|
Параметр |
|
|
Диаметр поршня |
76 |
|
Отношение радиуса кривошипа к длине шатуна |
0,26 |
|
Угол закрытия впускного клапана |
-125 |
|
Угол открытия выпускного клапана и |
123 |
|
Температура рабочего тела в начале такта сжатия |
288 |
|
Давление рабочего тела в начале такта сжатия |
101325 |
|
Коэффициент избытка воздуха |
1,05 |
|
Порядок химической реакции |
1,5 |
|
Коэффициент Пуассона для свежей смеси на стадии сжатия |
1,39 |
|
Коэффициент Пуассона для продуктов горения на стадии расширения |
1,23 |
|
Нормальная скорость пламени для смеси стехиометрического состава в момент зажигания |
0,35 |
|
Мольная стехиометрическая доля топлива, поступающего в камеру сгорания за один цикл, |
0,0186 |
|
Отношение энтальпии химической реакции к внутренней энергии системы для смеси стехиометрического состава в момент зажигания |
7,4 |
Интересно отметить, что частота вращения коленчатого вала ![]() также незначительно влияет на длительность процесса сгорания смеси, т.е. зависимость
также незначительно влияет на длительность процесса сгорания смеси, т.е. зависимость ![]() оказывается одинаковой при варьировании частоты вращения в широких пределах, что подтверждается также известными экспериментальными данными.
оказывается одинаковой при варьировании частоты вращения в широких пределах, что подтверждается также известными экспериментальными данными.
Автомодельность индикаторной диаграммы является результатом моделирования и объяснение может иметь следующее. Скорость турбулентного пламени, в основном, определяется скоростью турбулентного переноса, которая в свою очередь пропорциональна средней скорости поршня [8-10] и слабо зависит от нормальной скорости пламени. При увеличении частоты вращения увеличивается и скорость сгорания смеси. При этом длительность процесса сгорания в единицах угла поворота коленчатого вала остается практически неизменной.
Исследование влияния на показатели процесса угла опережения зажигания, степени сжатия и частоты вращения коленчатого вала ![]() показывает, что процессы в созданных моделях отражают процессы в реальном двигателе.
показывает, что процессы в созданных моделях отражают процессы в реальном двигателе.
Было исследовано влияние формы камеры сгорания на протекание рабочего процесса. При этом для его оценки использованы индикаторные диаграммы, полученные численным моделированием при ![]() .
.
Диаграммы сравнивались по двум параметрам: продолжительности сгорания и максимальному давлению в цилиндре.
На рис. 8 приведены индикаторные диаграммы для разных геометрий камеры сгорания (Модели 1 , 1А и 7). Видно, что в зависимости от формы камеры сгорания сильно изменяется продолжительность сгорания (наименьшая для Модели1 - симметричной камеры с точкой зажигания на оси). Время полного сгорания для двигателя с цилиндрической камерой сгорания со смещенной точкой зажигания ( Модель 1А) примерно в два раза больше (процесс сгорания смеси сильно затянут) чем время полного сгорания для симметричной камеры с точкой зажигания на оси; еще больше оно для клиновидной камеры с асимметричным зажиганием - (Модель 7). Полученные данные позволяют сделать вывод, что в Модели 7 и Модели 1А максимальное (и среднее) индикаторное давление значительно ниже, чем в Модели 1; зависимость динамики сгорания от частоты вращения ![]() весьма слабая.
весьма слабая.
Далее можно отметить, что нами проводились также исследования влияния формы камеры сгорания и положения точки зажигания на динамику сгорания и КПД цикла. Численные исследования показали, что КПД реальных циклов сгорания смеси значительно ниже, чем идеализированного цикла Отто. Зависимости КПД от частоты вращения слабая, от угла опережения зажигания сильная и имеет максимум при угле зажигания -20 град. п.к.в. для Модели 1, а для Модели 7 этот максимум расположен дальше от ВМТ (т.е. при угле зажигания -40 град. п.к.в.) и имеет значительно больший градиент на графике.
В заключение следует отметить, что путем численного моделирования в работе дано численное подтверждение факта заметного влияния на динамику сгорания смеси и индикаторный КПД цикла формы камеры сгорания и места расположения точки зажигания.
|
а) |
|
|
б) |
|
|
в) |
|
|
Модель1 (влияние Рис.2. Динамика давления при сгорании смеси в двигателе с искровым зажиганием при углах зажигания а) |
|
|
а) |
|
|
б) |
|
|
в) |
|
|
Модель1А (влияние Рис. 3. Динамика давления при сгорании смеси в двигателе с искровым зажиганием при углах зажигания а) |
|
|
а) |
|
|
б) |
|
|
в) |
|
|
Модель 7 (влияние Рис. 4. Динамика давления при сгорании смеси в двигателе с искровым зажиганием при углах зажигания а) |
|
|
а) |
|
|
б) |
|
|
в) |
|
|
Модель1 (влияние Рис. 5. Динамика давления при сгорании смеси в двигателе с искровым зажиганием при углах зажигания а) |
|
|
а) |
|
|
б) |
|
|
в) |
|
|
Модель1А (влияние Рис. 6. Динамика давления при сгорании смеси в двигателе с искровым зажиганием при углах зажигания а) |
|
|
а) |
|
|
б) |
|
|
в) |
|
|
Модель 7 (влияние Рис. 7. Динамика давления при сгорании смеси в двигателе с искровым зажиганием при углах зажигания а) |
|
|
а) |
|
|
б) |
|
|
Рис. 8. Динамика сгорания смеси в камерах с различной реальной геометрией а) |
|
СПИСОК Литературы